
Logic gates:
A computer is essentially an assembly of transistors and powered and unpowered circuits. A logic gate is made up of several transistors that are connected in series to produce one or more outputs, depending on the input or set of inputs that are supplied to it. There are three different gate kinds to think about:
- AND gate
- OR gate
- NOT gate
Every kind of gate has three different representations: an algebraic form, a diagram, or a truth table.
AND gates
An AND gate uses two inputs to generate one output. The output is 1 (true) only if both of the inputs are 1 (true). AND gates are represented diagrammatically as:
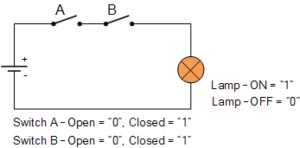
The initial input is represented by A. The second input is denoted by B. Q is the output.
A truth table displays the expected output for each set of inputs. Similar to logic gates, in the table, a 0 denotes FALSE and a 1 TRUE.
The truth table below shows a representation of an AND gate.
| Input | Output | |
| A | B | A AND B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR gates
An OR gate uses two inputs to generate one output. The output is 1 (TRUE) only if either or both of the inputs are 1 (TRUE).
OR gates are represented diagrammatically as:

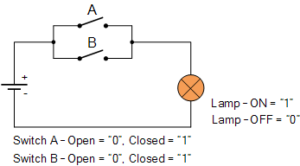
A represents the first input. B represents the second input. Q represents the output.
An OR gate is represented in the truth table below.
| Input | Output | |
| A | B | A OR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
NOT gates
A NOT gate uses just one input to generate one output. A NOT gate inverts the input; the output is 1 (TRUE) if the input is 0 (FALSE), and the output is 0 (FALSE) if the input is 1 (TRUE).
NOT gates are represented diagrammatically as:

The NOT gate has what appears to be a nose at the front. When using more complex gates, this nose is added to other gates to show they have been combined with the NOT gate.
A NOT gate is represented in the truth table below.
| A | Y |
| 0 | 1 |
| 1 | 0 |

